andre/the-swift-programming-language-in-chinese
1
0
Fork 0
Code Issues Pull Requests Packages Projects Releases Wiki Activity

修复字符串和字符, 集合类型, 函数章节的图片链接 (#1219)

Browse Source
This commit is contained in:
windorz9
2023-03-09 22:01:47 +08:00
committed by GitHub
parent ed0939a579
commit e31ea50e8f
3 changed files with 9 additions and 9 deletions
Download Patch File Download Diff File Expand all files Collapse all files

2
source/02_language_guide/03_Strings_and_Characters.md
View File

@ -460,7 +460,7 @@ let newString = String(beginning)
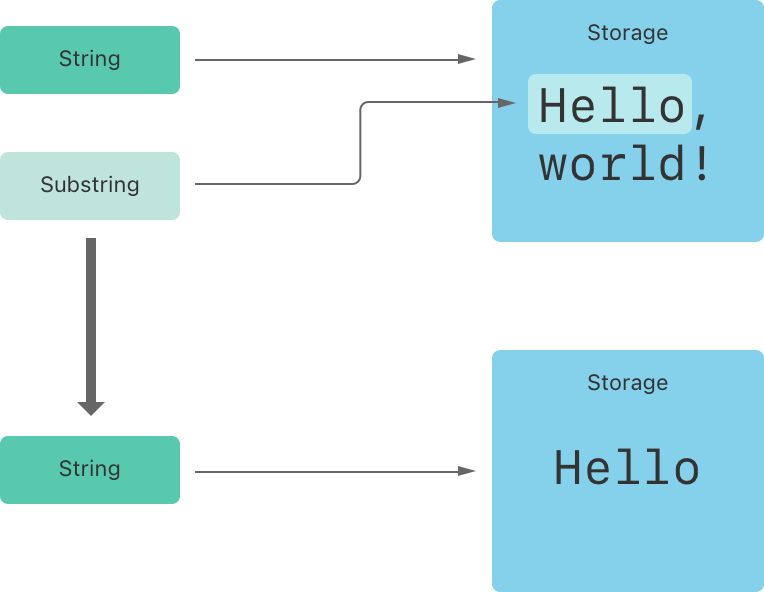
上面的例子，`greeting` 是一个 `String`，意味着它在内存里有一片空间保存字符集。而由于 `beginning` 是 `greeting` 的 `Substring`，它重用了 `greeting` 的内存空间。相反，`newString` 是一个 `String` —— 它是使用 `Substring` 创建的，拥有一片自己的内存空间。下面的图展示了他们之间的关系：
![](https://docs.swift.org/swift-book/_images/stringSubstring_2x.png)
![](https://docs.swift.org/swift-book/images/stringSubstring@2x.png)
> 注意
>

6
source/02_language_guide/04_Collection_Types.md
View File

@ -2,7 +2,7 @@
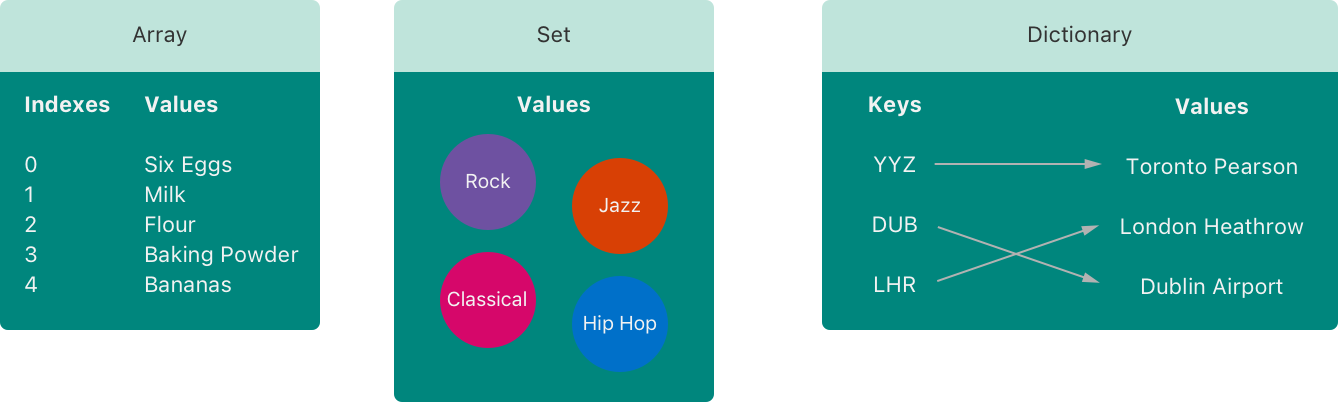
Swift 语言提供数组（Array）、集合（Set）和字典（Dictionary）三种基本的*集合类型*用来存储集合数据。数组是有序数据的集。集合是无序无重复数据的集。字典是无序的键值对的集。
![](https://docs.swift.org/swift-book/_images/CollectionTypes_intro_2x.png)
![](https://docs.swift.org/swift-book/images/CollectionTypes_intro~dark@2x.png)
Swift 中的数组、集合和字典必须明确其中保存的键和值类型，这样就可以避免插入一个错误数据类型的值。同理，对于获取到的值你也可以放心，其数据类型是确定的。
@ -401,7 +401,7 @@ for genre in favoriteGenres.sorted() {
下面的插图描述了两个集合 `a` 和 `b`，以及通过阴影部分的区域显示集合各种操作的结果。
![](https://docs.swift.org/swift-book/_images/setVennDiagram_2x.png)
![](https://docs.swift.org/swift-book/images/setVennDiagram@2x.png)
* 使用 `intersection(_:)` 方法根据两个集合的交集创建一个新的集合。
* 使用 `symmetricDifference(_:)` 方法根据两个集合不相交的值创建一个新的集合。
@ -427,7 +427,7 @@ oddDigits.symmetricDifference(singleDigitPrimeNumbers).sorted()
下面的插图描述了三个集合 `a`、`b` 和 `c`，以及通过重叠区域表述集合间共享的元素。集合 `a` 是集合 `b` 的*父集合*，因为 `a` 包含了 `b` 中所有的元素。相反的，集合 `b` 是集合 `a` 的*子集合*，因为属于 `b` 的元素也被 `a` 包含。集合 `b` 和集合 `c` 是*不相交*的，因为它们之间没有共同的元素。
![](https://docs.swift.org/swift-book/_images/setEulerDiagram_2x.png)
![](https://docs.swift.org/swift-book/images/setEulerDiagram@2x.png)
* 使用“是否相等”运算符（`==`）来判断两个集合包含的值是否全部相同。
* 使用 `isSubset(of:)` 方法来判断一个集合中的所有值是否也被包含在另外一个集合中。

10
source/02_language_guide/05_Control_Flow.md
View File

@ -120,7 +120,7 @@ while condition {
下面的例子来玩一个叫做*蛇和梯子*（也叫做*滑道和梯子*）的小游戏：
![image](https://docs.swift.org/swift-book/_images/snakesAndLadders_2x.png)
![image](https://docs.swift.org/swift-book/images/snakesAndLadders@2x.png)
游戏的规则如下：
@ -422,7 +422,7 @@ default:
// 输出“(1, 1) is inside the box”
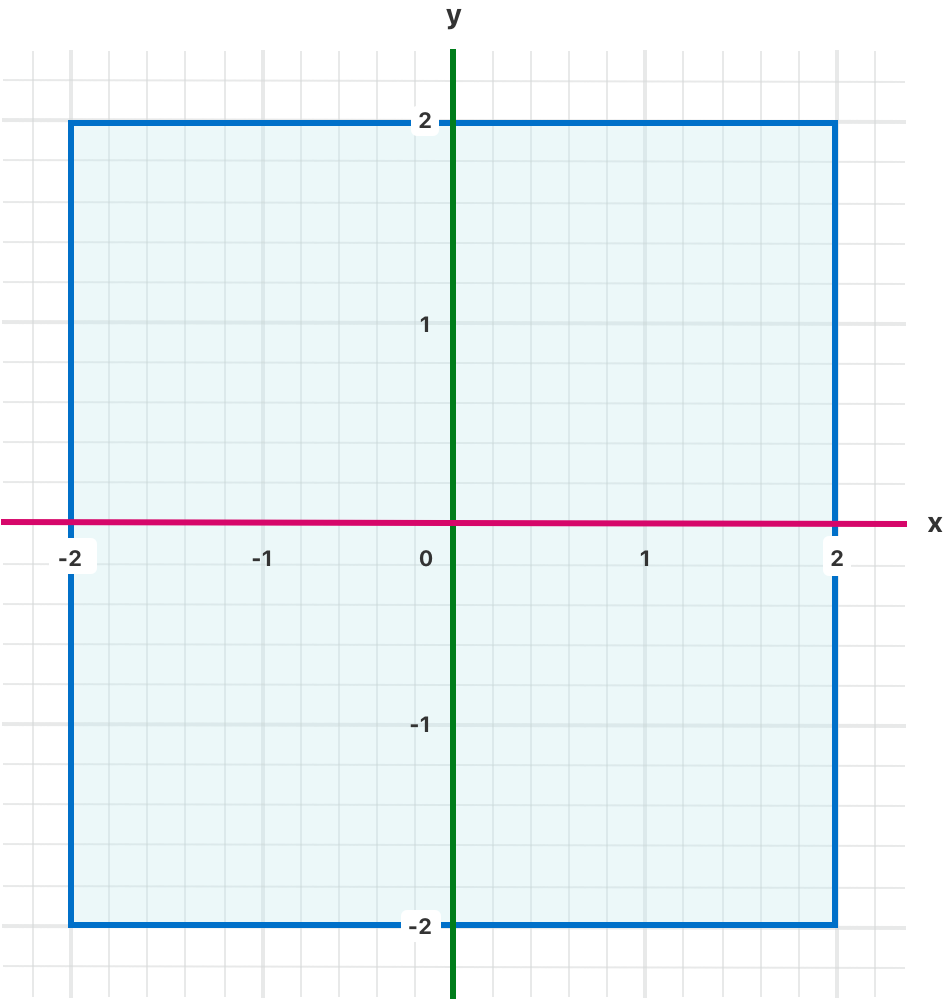
```
![image](https://docs.swift.org/swift-book/_images/coordinateGraphSimple_2x.png)
![image](https://docs.swift.org/swift-book/images/coordinateGraphSimple@2x.png)
在上面的例子中，`switch` 语句会判断某个点是否是原点 (0, 0)，是否在红色的 x 轴上，是否在橘黄色的 y 轴上，是否在一个以原点为中心的4x4的蓝色矩形里，或者在这个矩形外面。
@ -447,7 +447,7 @@ case let (x, y):
// 输出“on the x-axis with an x value of 2”
```
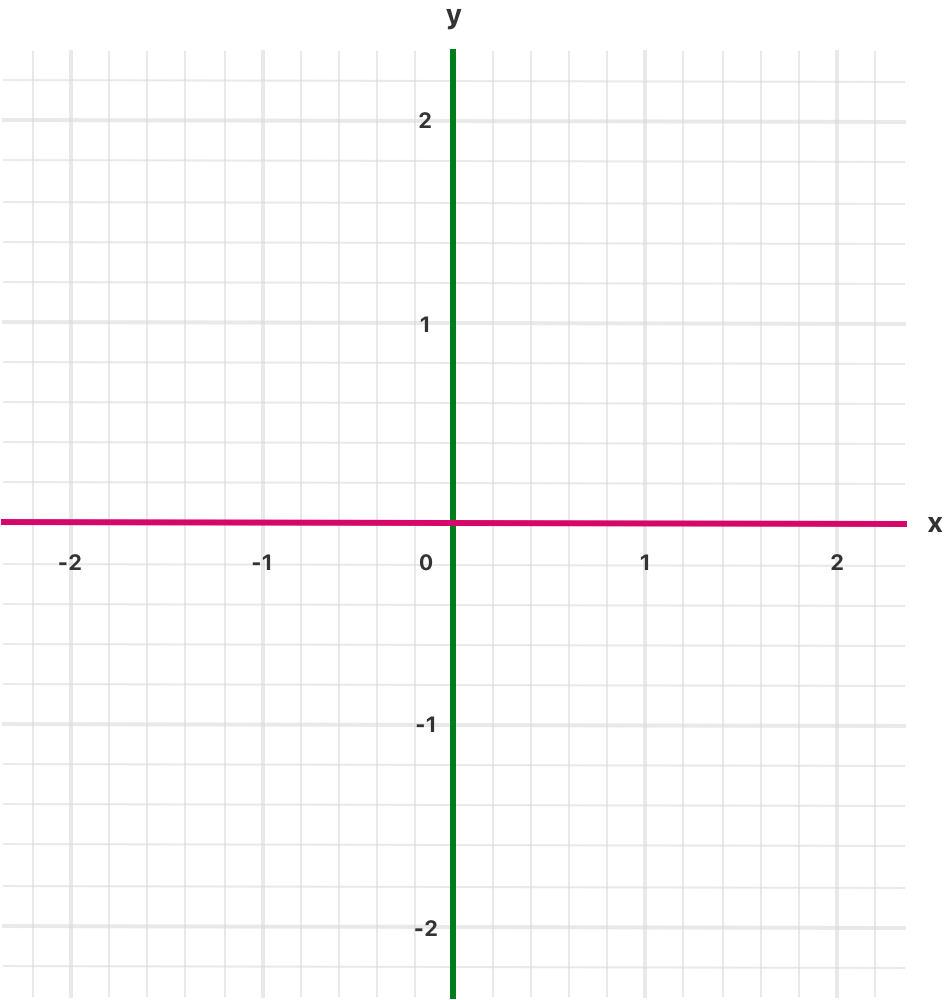
![image](https://docs.swift.org/swift-book/_images/coordinateGraphMedium_2x.png)
![image](https://docs.swift.org/swift-book/images/coordinateGraphMedium@2x.png)
在上面的例子中，`switch` 语句会判断某个点是否在红色的 x 轴上，是否在橘黄色的 y 轴上，或者不在坐标轴上。
@ -476,7 +476,7 @@ case let (x, y):
// 输出“(1, -1) is on the line x == -y”
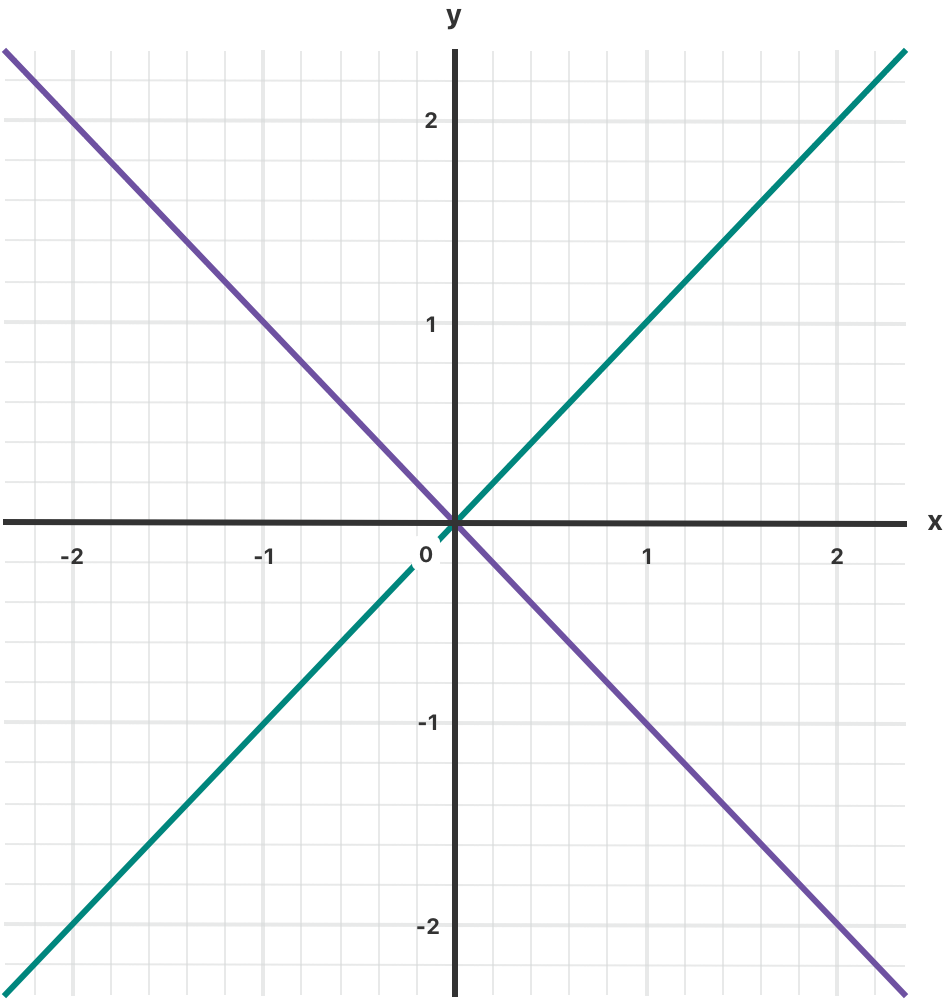
```
![image](https://docs.swift.org/swift-book/_images/coordinateGraphComplex_2x.png)
![image](https://docs.swift.org/swift-book/images/coordinateGraphComplex@2x.png)
在上面的例子中，`switch` 语句会判断某个点是否在绿色的对角线 `x == y` 上，是否在紫色的对角线 `x == -y` 上，或者不在对角线上。
@ -655,7 +655,7 @@ print(description)
游戏的棋盘和之前一样：
![image](https://docs.swift.org/swift-book/_images/snakesAndLadders_2x.png)
![image](https://docs.swift.org/swift-book/images/snakesAndLadders@2x.png)
`finalSquare`、`board`、`square` 和 `diceRoll` 值被和之前一样的方式初始化：